PID with Haply

For our third lab (or fourth?) in the CanHap course, we were asked to play with using PID to move the haply to a given position. With the haply, we can set the amount of torque to be applied and get the current position of the arms, which will help us calculate the position of the end-effector. Since we can directly set the position, the use of PID makes sense for this situation. We were given an implementation of the PID controls with a GUI configure the parameters of the PID controller. Initially, the coefficients of proportion (P), integral (I), and derivative (d) were set to zero and were instructed to try adjusting the P, I and D coefficients respectively (which is usually the order in which they are tuned) to understand how PID works.

All the code for this is on my github.

On a high level, the P component is primary component of the controller, which is basically the euclidean distance of the end-effector from the target location. The torque applied is proportional to this error (distance). The problem with using only this is that it tends to overshoot the target and results in the system oscillating around the target state. The I term is meant to reduce this oscillation. When the system is oscillating, this I term accumulates and torque proportional to this term is applied which eventually eliminates (or attenuates) the oscillation. Another problem that can occur with these systems is that large correction signals (distance or accumulated error) can throw the system into an unstable state. The D component is used to alleviate this. Basically, it dampens the signal at a rate proportional to the signal itself. This component can be further augmented by smoothing the dampening signal over the last few error signals (which I learned from the code itself).

So the idea of the lab is to see this in action. Right out the game, when I tried making even small adjustments to the P value, the whole systems starts to freak out. Playing around with the code and P5 library, what I wound up is adding a few additional outputs, a button and keybindings for convenience. I added a keybinding (“z” in my case) to reset the errors and PID coefficients to their respective initial values, and I added an output showing the values for the coefficients and the torque values being set. I wound up using these two alot to get a sense of what is going on and go through the lab task better. Every time the haply loses it’s position, I’d hit “z” and then “i” (which resets the haply’s position) then continue playing. Occasionally, the values are thrown into “NaN” values (which I didn’t put effort into fixing); other than that I was able to do everything quite smoothly (sans the haply’s breakdowns). The following clip shows the changes I made to the UI.

Another trick I used for experimenting is to move the end-effector to the target and again hit “z” (reset coefficients and errors) after resetting the complete system (coefficients, errors, and haply’s position). Then repeatedly hit “b”, moves the target to a different location and the haply is forced to move to that location.

The P

One of the first things I tried with the P values is to gradually increase the P and see how far I can push the end-effector without putting in too much effort. The following shows how far the end-effector moves as P is increased, starting from 0.

When using only the P component, the haply tends to overshoot and loses it’s position easily. On the rare occasion that it doesn’t, it’s not exactly on the target location. Which means the I and D components are necessary to arrive at a stable system.

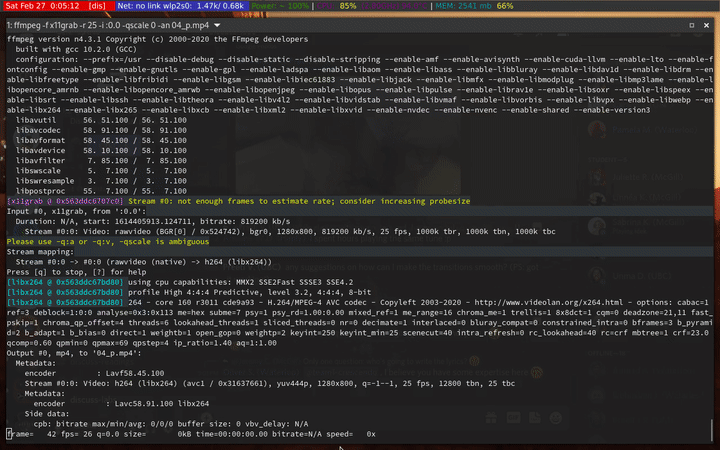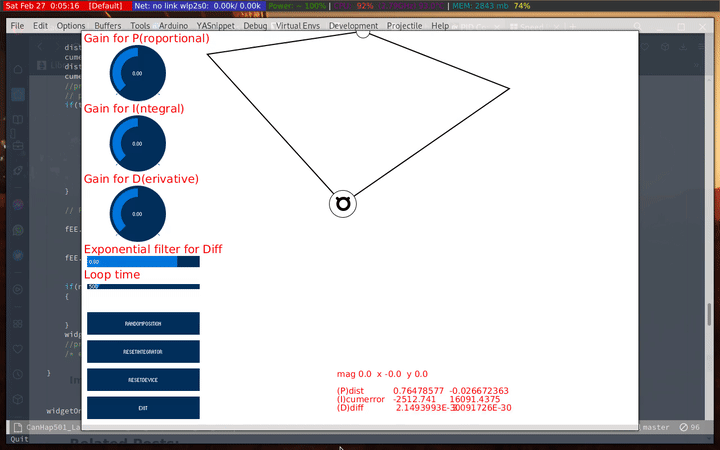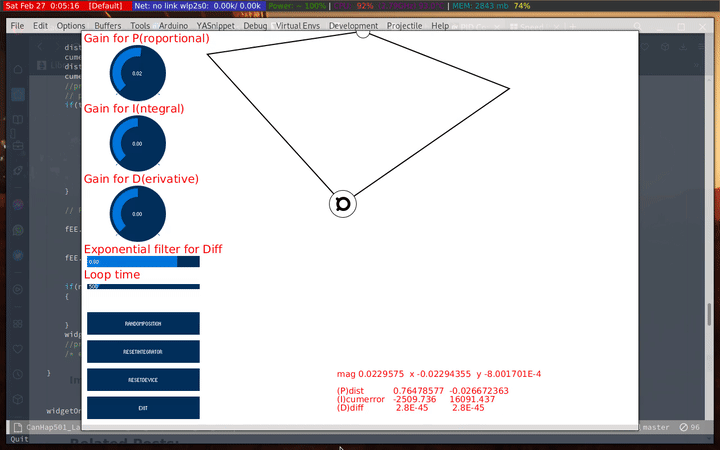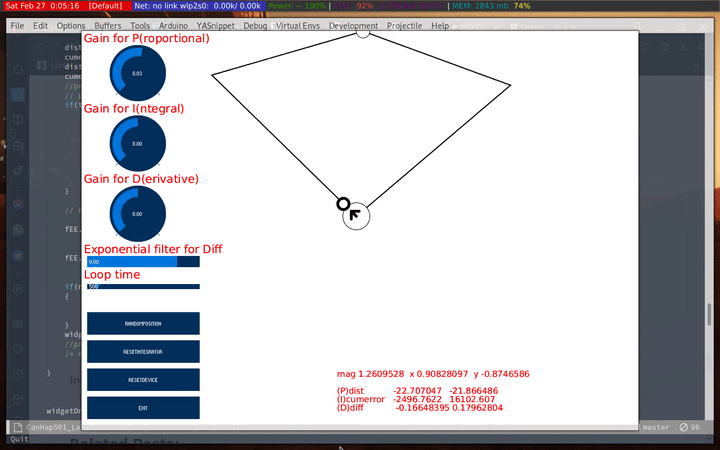
The I

I wanted to see how the I changed with time. I set P to 0, and adjusted I to see how it effects the force vector:

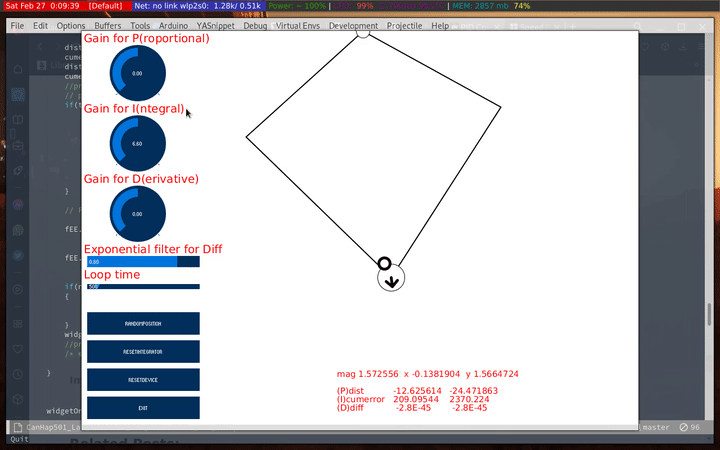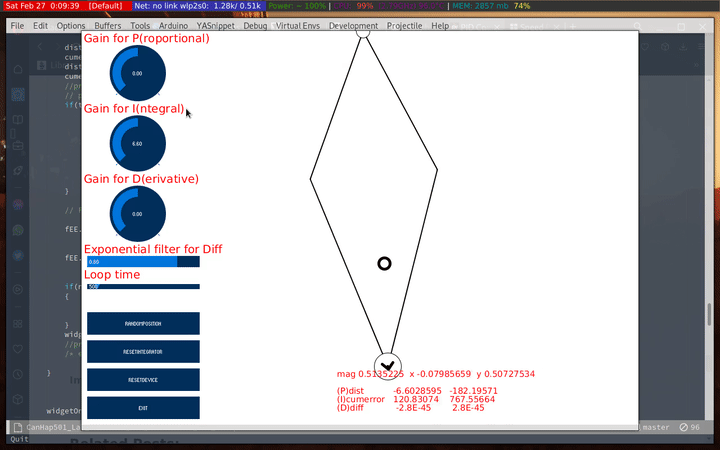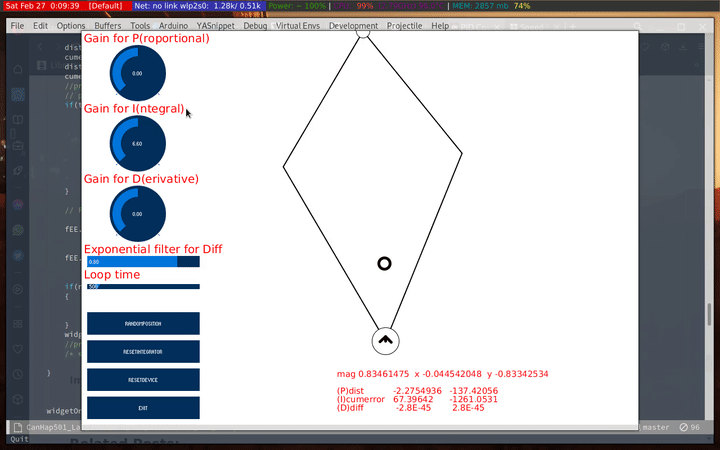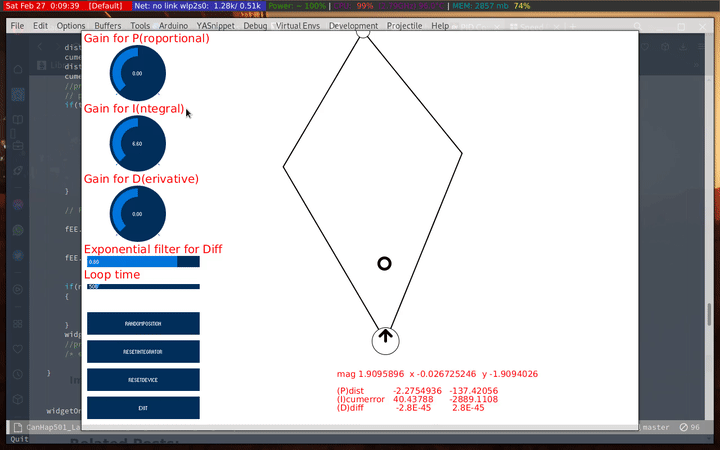
Following that I tried moving the target points around to see how it behaves. It was much better than using only P, but still tends to overshoot and lose track of the haply’s position.

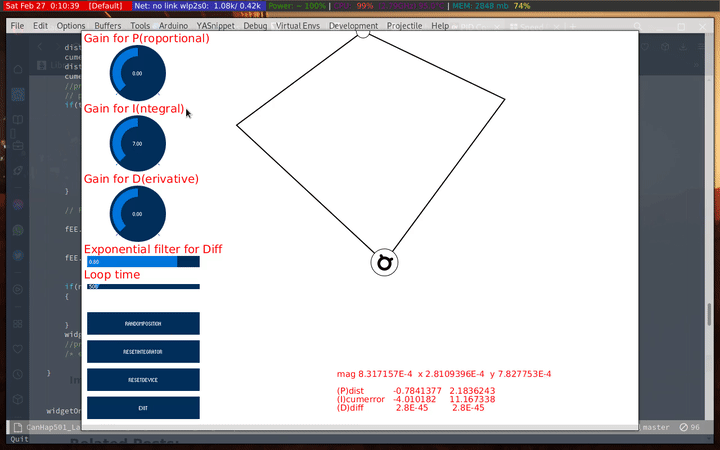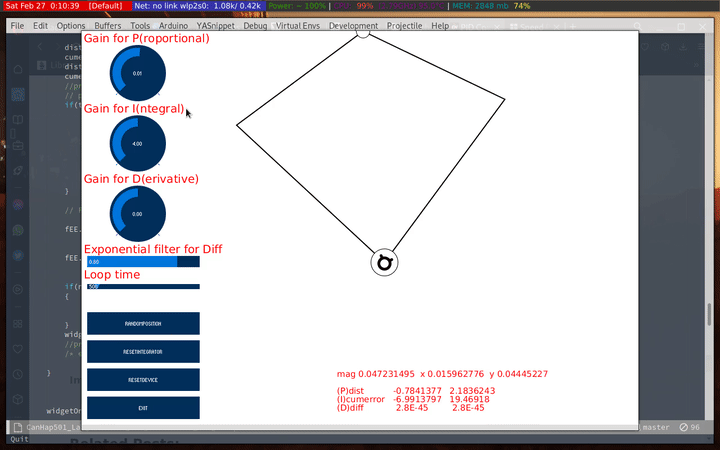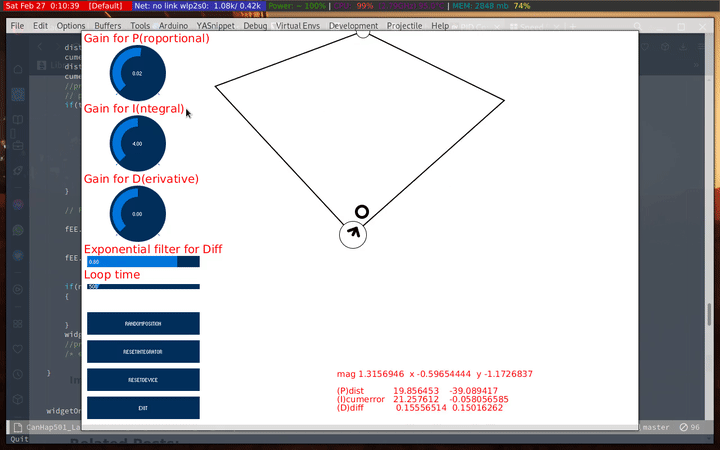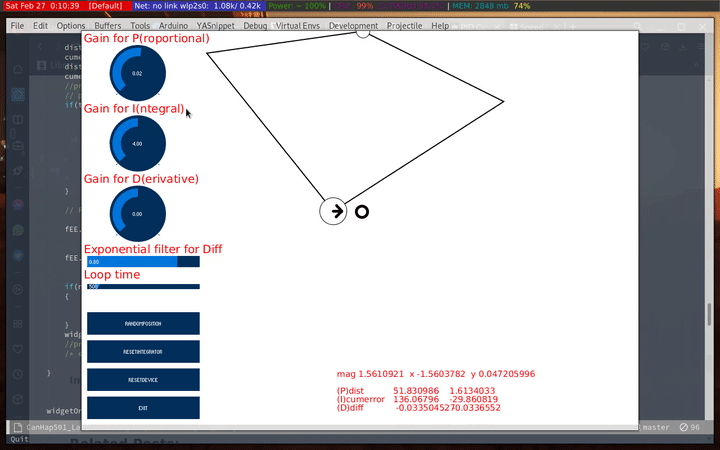
While it was fun to watch that, I found this behavior I though was interesting. Basically, the haply constrains my movements along the x-axis. What I basically had done is let the I accumulate over the y axis and set the smoothing to 99%. I don’t entirely understand what causes that, but I thought it was something interesting.

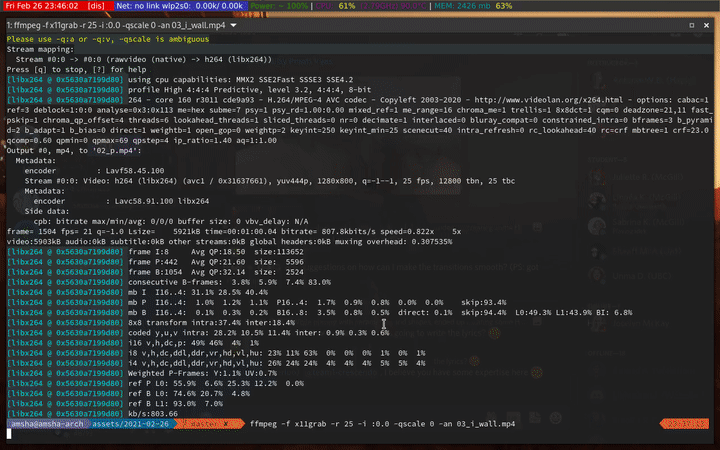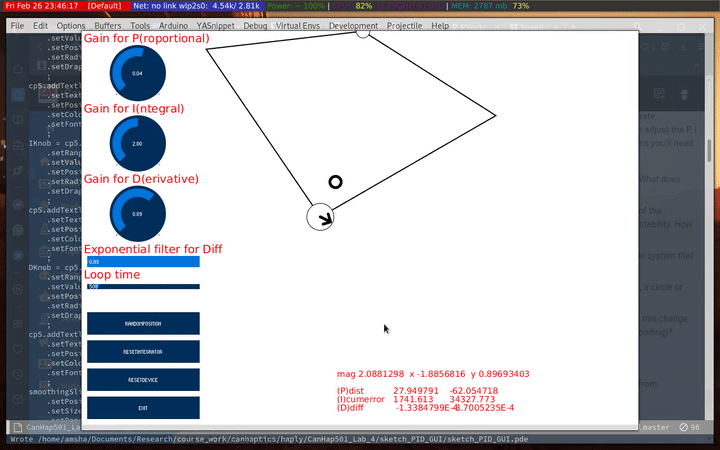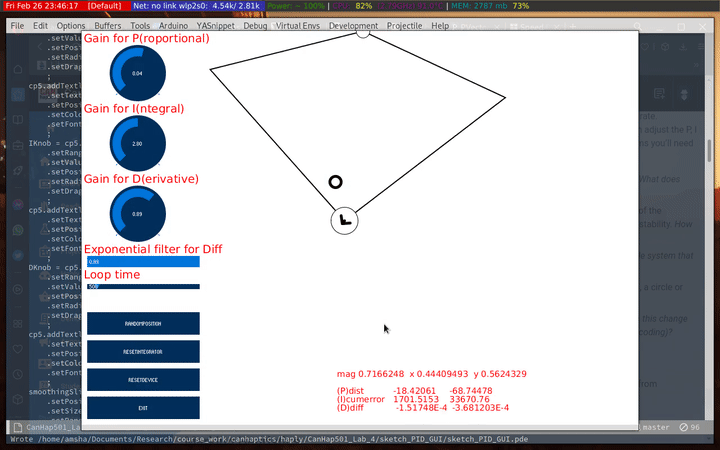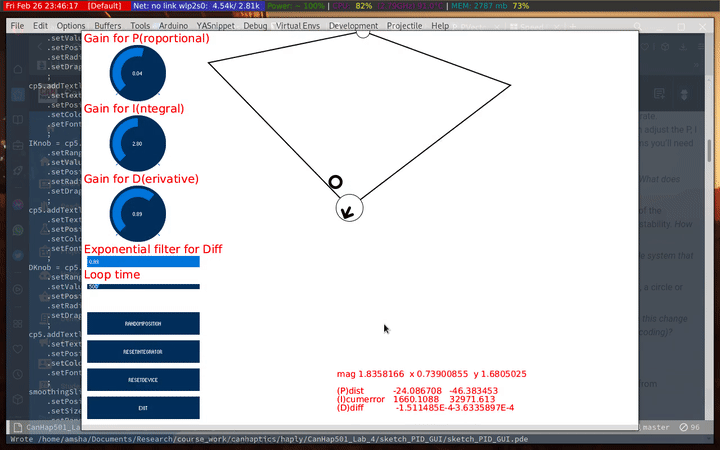
The D

I tried different configuration and settled for the following ranges:

• P: 0.03 - 0.04
• I: 5 - 6
• D: 1.0 - 1.1
• smoothing ~ 0.5

Continuous PID

To asses how the system behaves when following a path, I added a option to switch to having the target follow a circular path. And the end-effector is expected to follow the target.

When I hold back the end-effector, the force applied sensed increases gradually as the target moves away. Additionally, the D component drops to 0, as there is virtually no movement, and the I component accumulates quite a bit as I am holding it down for a bit. But the parameters were stable enough that when I let go it snaps back to following the path.

Looptime

When I increase the loop time the system tends to lose control more often. It was more preferable to have the looptime at a lower rate. When the looptime is set to anything above 1000, the haply’s arms locks up whenever it reaches a point towards the outside edge of the device, causing the instability. Also, the lower frame-rates results in jerky motions as the PID has to accommodate a larger distance for each frame.

Final thoughts

Overall, it was fun to see the PID being applied to the haply to move it to a given location. And at the end of the day, the device is still in one piece, which is a win-win.